[AI] Decision Tree, 엔트로피, 정보 이득, 정보이득비, 지니 지수

결정 트리는, 트리 형태로 의사결정 지식을 표현하는 것을 말합니다.

위의 예시는, 날씨가 어떨 때 테니스를 치러 갈까? 를 결정하는 의사결정 트리인데요,

쉽게 말해 Internal Node는, 기상 상황들을 말하는 것이고,

Edge는 그 기상 상황이 어떤지, 즉 속성값을 나타냅니다.

그리고 마지막 Terminal node는, 부류. 여기서는 Yes or No를 나타냅니다.

 

결정 트리 알고리즘을 구성하는 것은, 

- 우선 하나의 노드로 구성된 트리에서 시작합니다.

1. 분할 속성을 선택하고,

2. 속성값에 따라서 서브트리를 확장 및 생성하고,

3. 데이터를 속성값에 따라 분배합니다.

이 1-2-3 과정을 반복합니다.

 

우리는 일반화 성능이 우수한 최대한 간단한 트리를 원합니다. 

 

방금, 결정 트리 알고리즘을 구성할 때, 분할 속성을 선택한다고 했는데, 

이 때 어떤 속성을 선택하는 것이 좋을까요?

분할한 결과가 순도가 높은, 동질적인, 동일한 부류를 가지는 것으로 만드는 속성을 선택하는 것이 좋습니다.

 

이 때, 순도를 측정하는 척도가 바로 엔트로피 입니다.

엔트로피는, 보편적인 의미로 무질서의 척도라고들 하잖아요?

여기서도 개념은 비슷합니다. 엔트로피는 순도와 반비례 해요. 불순도와 비례합니다.

 

그래서, 엔트로피가 낮은 분할 속성을 선택하는 것이 우수한 것이죠. 

 

전체의 절반이 T고, 나머지 절반이 F라면 이것의 순도는 어떨까요?

반반이니 순도는 50이라고 표현할 수 있겠습니다.

두 부류로 나뉠 때 순도에서의 최악은 50이죠. 엔트로피 값은 이 때 최상입니다.

 

그리고, 데이터가 세 부류로 나뉘는데

각각 1/3씩 나뉘면? 이 때도 엔트로피가 최상이고, 순도는 최악입니다.

정보이득: 부모 - 자식 간 엔트로피의 차이

어떤 기준에 따라 서브트리를 생성하고, 그게 우수한 분할 속성이었는지? 를 판단하는 지표인데요,

부모 - 자식 간 엔트로피 차이가 클 수록 우수한 분할 속성으로 판단합니다.

 

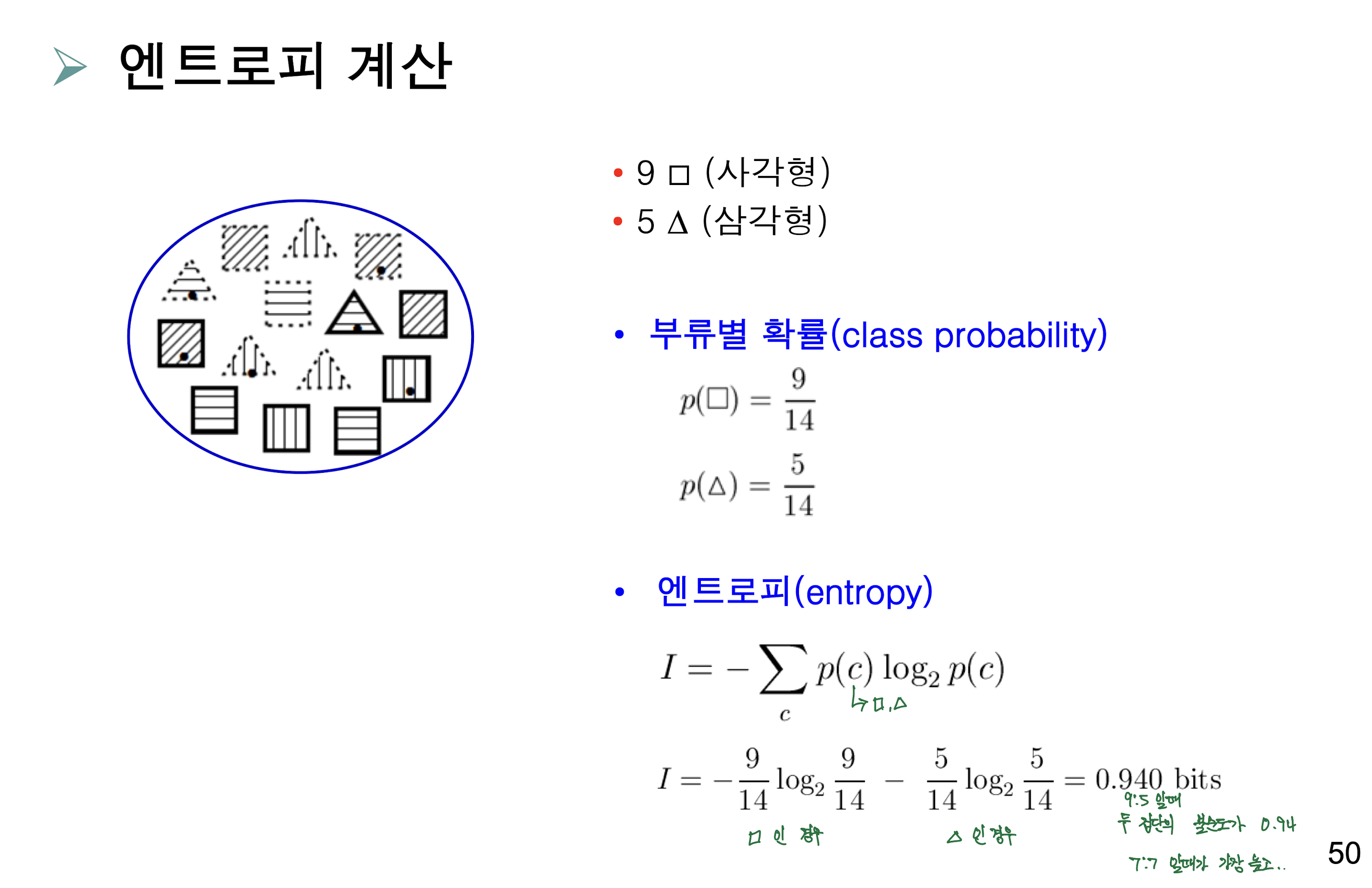
삼각형과 사각형으로 분류하는 문제인데요, 

가령, 원본 데이터가 저렇고, 속성(패턴)에 따라 서브트리를 생성하면,

그리고 계산식에 따라 진행해주면 최종 IG(정보이득)값이 계산됩니다. 

 

패턴 속성을 기준으로 나누는 것이 IG가 가장 크니까, 첫번째 서브트리를 생성할 떄는 패턴을 기준으로 하고

나머지 속성들은 그 뒤에 적용합니다.

처음에는 Outline이 지금의 Dot 자리에도 적용될 거라 생각했는데

그렇지 않고 각 속성은 한 번씩만 사용됩니다.

그래서 이러한 최종 결정 트리가 생성됩니다.

 

이런 IG 척도에는 단점이 있는데요,

자식 세대에 분리한 이후 순도가 높을 수록 엔트로피가 작아지니, IG값도 커지는데요

속성값이 많아지면, 부분집합의 크기가 작아지면서

그러니까 쉽게 말하면 IG값이 좋은 것만 찾다가는 Overfit 된, 일반화 성능이 떨어지는 트리가 나온다는 것입니다.

 

그래서 그 개선책으로, 정보이득비(IG ratio) 척도라는 것이 있고, 지니 지수(Gini index)라는 척도가 있는데요, 

첫번째로, 정보이득비의 경우

속성값이 너무 많은 것을 고르면, 패널티를 주도록 합니다.

여기서 I(Pattern)는, 속성값(패턴)을 부류로 간주하여 계산한 엔트로피로, 속성값이 많아질 수록 그 값이 커지구요

GainRatio(Pattern)은 IG값을 I값으로 나눠줌으로서

속성값이 많아질 때 패널티가 생기도록 하는 것입니다.

 

결론적으로는 속성값이 많아서 정보이득 값이 좀 높았던 패턴의 경우는

속성의 개수에 따라 패널티를 줘서, 상대적으로 이득비는 줄어들게 되었네요.

 

그 다음 지니 지수인데요, 그냥 집단 안에서 속성값을 부류라고 생각하고..

부모 지니값과 자식 지니값의 차를 지니 지수 이득으로 봐서 계산하는 것이네요.